Merkle Trees in Practice: A Deep Dive into Implementation and Optimisation

Merkle Trees: The Data Structure for Verifiable State

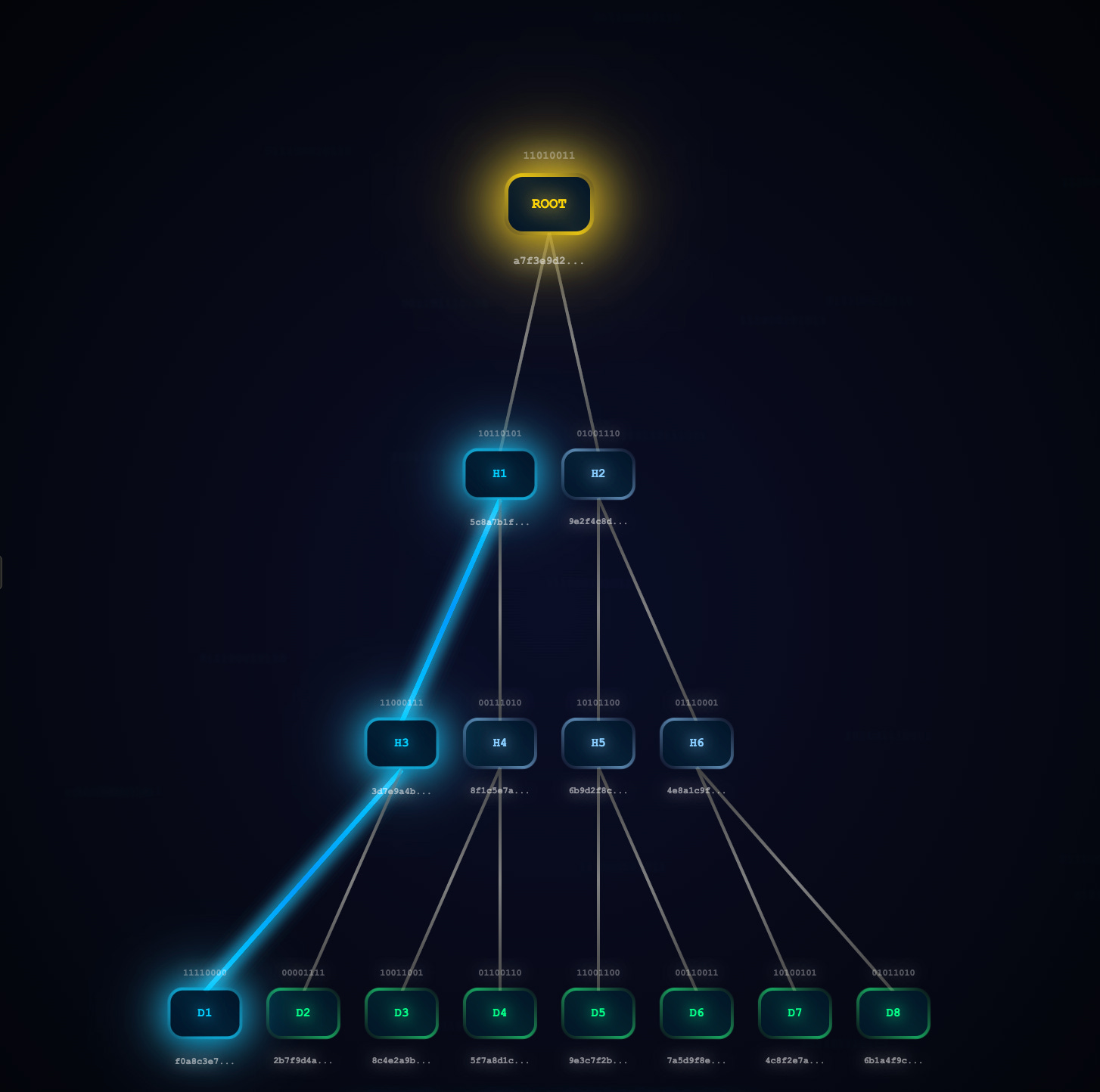
In our last post, we discussed about how you can compare two large datasets for integrity using Merkle trees.

The beauty of Merkle Trees lies in their efficiency: you can verify that a specific piece of data belongs to a larger dataset by providing just a small "proof" - a path of hashes from the leaf to the root, rather than the entire dataset.

In this post, let’s dive into the implementation details and understand how we can leverage Merkle trees in real-world.

Naive Implementation

Let’s start with a naive implementation for Merkle Trees.

Core Structure

type Node struct {
    Hash  []byte
    Data  []byte  // Only populated for leaf nodes
    Left  *Node
    Right *Node
}

type MerkleTree struct {
    Root   *Node
    Leaves []*Node
}

The structure is straightforward - each node contains a hash and optional data (populated only for leaf nodes), with pointers to left and right children. The Merkle Tree maintains references to both the root and all leaf nodes.

Tree Construction Process

The construction follows these steps:

1. Create Leaf Nodes: Each data block is hashed using SHA-256

2. Build Tree Bottom-Up: Recursively combine pairs of nodes

3. Handle Odd Numbers: Duplicate the last node in case of odd number of nodes

4. Combine Hashes: Concatenate child hashes and hash the result

func buildTreeRecursive(nodes []*Node) *Node {
    if len(nodes) == 1 {
        return nodes[0]
    }

    // Handle odd number of nodes by duplicating the last one
    if len(nodes)%2 == 1 {
        nodes = append(nodes, nodes[len(nodes)-1])
    }

    // Build parent level by combining pairs
    parentLevel := make([]*Node, 0)
    for i := 0; i < len(nodes); i += 2 {
        left := nodes[i]
        right := nodes[i+1]

        combinedHash := append(left.Hash, right.Hash...)
        hash := sha256.Sum256(combinedHash)

        parent := &Node{
            Hash:  hash[:],
            Left:  left,
            Right: right,
        }
        parentLevel = append(parentLevel, parent)
    }

    return buildTreeRecursive(parentLevel)
}

Proof Generation

The proof generation attempts to create a path from a leaf to the root by collecting sibling hashes at each level. This allows someone to verify a piece of data belongs to the tree without having the entire dataset.

func (mt *MerkleTree) GenerateProof(index int) ([][]byte, error) {
	if index < 0 || index >= len(mt.Leaves) {
		return nil, errors.New("index out of range")
	}

	proof := make([][]byte, 0)

	// Navigate from leaf to root, collecting sibling hashes
	currentIndex := index
	currentLevel := mt.Leaves

	for len(currentLevel) > 1 {
		// Handle odd number of nodes
		if len(currentLevel)%2 == 1 {
			currentLevel = append(currentLevel, currentLevel[len(currentLevel)-1])
		}

		// Find sibling
		var siblingIndex int
		if currentIndex%2 == 0 {
			siblingIndex = currentIndex + 1
		} else {
			siblingIndex = currentIndex - 1
		}

		proof = append(proof, currentLevel[siblingIndex].Hash)

		// Move to parent level
		currentIndex = currentIndex / 2

		// Rebuild parent level
		parentLevel := make([]*Node, 0)
		for i := 0; i < len(currentLevel); i += 2 {
			parentLevel = append(parentLevel, findParent(currentLevel[i], currentLevel[i+1], mt.Root))
		}
		currentLevel = parentLevel
	}

	return proof, nil
}

While the naive implementation is good enough to demonstrate how Merkle trees work, it isn’t good enough to be used in the real-world.

Let’s dive into the problems with this existing implementation and what we can do to overcome it.

Problems with Naive Implementation

Broken Proof Verification

func VerifyProof(dataBlock []byte, proof [][]byte, rootHash []byte) bool {
    hash := sha256.Sum256(dataBlock)
    currentHash := hash[:]

    for _, siblingHash := range proof {
        // We don't know if sibling is left or right!
        combinedHash1 := append(currentHash, siblingHash...)
        hash1 := sha256.Sum256(combinedHash1)

        combinedHash2 := append(siblingHash, currentHash...)
        _ = sha256.Sum256(combinedHash2)  // This is never used!

        // We'll need to try both possibilities when verifying
        // This is clearly not ideal!
        currentHash = hash1[:]
    }

    return string(currentHash) == string(rootHash)
}

The Problem: The function computes both possible hash combinations (current+sibling and sibling+current) but only uses the first one. This means verification will fail roughly 50% of the time, even for valid proofs.

The fundamental issue stems from how cryptographic hash functions work: Hash(A + B) ≠ Hash(B + A). Hence we need to understand the correct order, to be able to confirm if its a valid proof.

The Solution: Proofs must include directional information (left/right).

Inefficient Proof Generation

func findParent(left, right, root *Node) *Node {
    if root == nil {
        return nil
    }

    if root.Left == left && root.Right == right {
        return root
    }

    if found := findParent(left, right, root.Left); found != nil {
        return found
    }

    return findParent(left, right, root.Right)
}

The Problem: For each level of the tree, the code performs a full tree traversal using findParent. This creates O(n²) complexity instead of the expected O(log n).

The Solution: Navigate directly from leaf to root using parent pointers will allow us better time complexity of O(log n).

Memory Inefficiency

The implementation stores complete subtrees during proof generation:

// Rebuild parent level
parentLevel := make([]*Node, 0)
for i := 0; i < len(currentLevel); i += 2 {
    parentLevel = append(parentLevel, findParent(currentLevel[i], currentLevel[i+1], mt.Root))
}
currentLevel = parentLevel

The Problem: This reconstructs entire tree levels in memory, consuming O(n) space for what should be an O(log n) operation.

Improved Implementation

Fixed Proof Verification with Directional Information

The Problem: The original implementation couldn't determine whether a sibling hash should be on the left or right during verification, leading to ~50% failure rate.

The Solution: Introduced ProofElement structure with explicit directional information:

type ProofElement struct {
    Hash   []byte
    IsLeft bool // true if this hash should be on the left during verification
}

O(log n) Proof Generation with Parent Pointers

The Problem: Original implementation used O(n²) tree traversals for each proof generation.

The Solution: Added parent pointers and direction flags to enable direct navigation:

type Node struct {
    Hash   []byte
    Data   []byte
    Left   *Node
    Right  *Node
    Parent *Node  // Added for efficient navigation
    IsLeft bool   // Track position in parent
}

Memory Efficiency and Resource Management

The Problem: Original implementation rebuilt entire tree levels in memory.

The Solution: Direct navigation eliminates unnecessary memory allocation:

func (mt *MerkleTree) GenerateProof(index int) ([]ProofElement, error) {
	if index < 0 || index >= len(mt.Leaves) {
		return nil, fmt.Errorf("index %d out of range [0, %d)", index, len(mt.Leaves))
	}

	proof := make([]ProofElement, 0)
	current := mt.Leaves[index]

	// Navigate from leaf to root using parent pointers - O(log n)
	for current.Parent != nil {
		parent := current.Parent
		var sibling *Node

		// Get sibling node
		if current.IsLeft {
			sibling = parent.Right
		} else {
			sibling = parent.Left
		}

		// Add sibling to proof with correct direction
		proof = append(proof, ProofElement{
			Hash:   sibling.Hash,
			IsLeft: !current.IsLeft, // Sibling's position relative to current
		})

		current = parent
	}

	return proof, nil
}

Secure Cryptographic Operations

The Problem: Original used string comparison for hashes, vulnerable to timing attacks.

The Solution: Implemented constant-time comparison and proper hash handling:

func VerifyProof(dataBlock []byte, proof []ProofElement, rootHash []byte) bool {
	if dataBlock == nil || rootHash == nil {
		return false
	}

	// Start with hash of the data block
	hash := sha256.Sum256(dataBlock)
	currentHash := hash[:]

	// Apply each proof element with correct ordering
	for _, element := range proof {
		var combinedHash []byte

		if element.IsLeft {
			// Sibling hash goes on the left
			combinedHash = make([]byte, 0, len(element.Hash)+len(currentHash))
			combinedHash = append(combinedHash, element.Hash...)
			combinedHash = append(combinedHash, currentHash...)
		} else {
			// Sibling hash goes on the right
			combinedHash = make([]byte, 0, len(currentHash)+len(element.Hash))
			combinedHash = append(combinedHash, currentHash...)
			combinedHash = append(combinedHash, element.Hash...)
		}

		hash := sha256.Sum256(combinedHash)
		currentHash = hash[:]
	}

	// Use constant-time comparison to prevent timing attacks
	return subtle.ConstantTimeCompare(currentHash, rootHash) == 1
}

A timing attack exploits variations in execution time to infer information about secret data being processed. The attack works because many algorithms have execution paths that depend on the data being processed - and these timing differences can leak information about that data.

An attacker could:

1. Generate fake proofs with different root hash candidates

2. Measure verification time for each candidate

3. Extract the real root hash byte by byte based on timing differences

Now with the improved implementation, let’s check with how much improvement we have gained:

Naive Implementation

Improved Implementation

As we can see, we can see a huge improvement in proof function because of the changes above. You can see a huge increase in performance in the optimised version:

Tree Size → Speedup Factor

100 → 253x

1,000 → 13,500x

10,000 → 103,400x

100,000 → 60,300x

These are just basic optimisations that bring our implementation closer to a production implementation. However, we can do more(let me know in comments if you want me to go into that).

Hopefully this article along with the previous one, gave you a good insight and understanding into Merkle Trees and how they can be implemented in the real-world.

Feel free to drop me a feedback!

👉 Connect with me here: Pratik Pandey on LinkedIn

👉 Find the code on Github here: Merkle Trees