Clocks: Logical Clocks
Logical clocks represent time through a virtual implementation, that represents a monotonically increasing value.
Prerequisites:
In my last article, we learned that despite physical clock synchronization using NTP servers, we might still see a clock skew of around 10ms. What it means is that if you’re trying to build a high throughput distributed system, where the ordering of operations is critical, you might face issues in correctly ordering the operations because of clock skew.
Logical Clocks
As the name suggests, logical clocks represent time through a virtual implementation, that represents a monotonically increasing value.
The easiest example could be taking an integer, which can be incremented every new operation to represent the ordering of operations. As such, we are just counting the number of operations that have occurred & since we use a monotonically increasing value for each operation, we’ll be able to establish causality across operations.
Now, that we know at a high level about logical clocks, let's go into different types of logical clocks -
Lamport Clocks
We talked about happens-before relationships in our previous articles on Strong Consistency Models. We covered total ordering and causal ordering between operations. Causality between operations establishes a dependency between them, where operation 2 may be dependent on the state caused by operation 1. Leslie Lamport suggested a solution to use logical timestamps to track happens-before relationships(Refer to his paper — Time, Clocks and Ordering Of Events). So this technique of using logical timestamps to track causality is named the Lamport Timestamp.
The algorithm suggested by Leslie talks about maintaining an individual counter per node/process.
Following are the steps followed by the algorithm -
Initialize the value of the counter to X, for each node/process.
For every event that a node/process receives locally, it increments the counter.
Each node/process can also send an event to another node/process. Before sending an event to another node/process, the counter is incremented and the incremented value of the counter is passed along with the event/message i.e. (Ci, M).
Each node when receiving a message/event from another node i.e. (Ci, M), checks the counter value Ci and updates its counter value Cj to MAX(Ci, Cj) + 1 & then delivers the message to the concerned application.
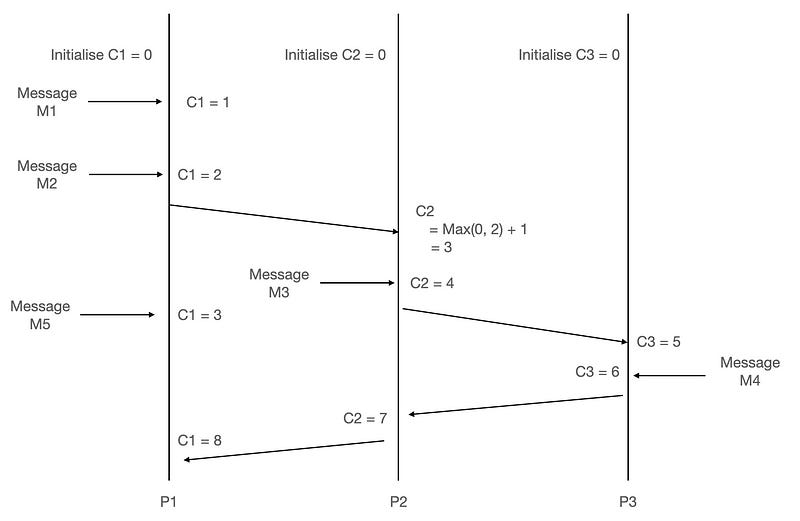
Using the above image, we can derive the following -
If A happens before B in the same process, then C(A) < C(B) is always true.
If A represents sending a message from Process P1, and B represents receiving the message by Process P2, based on the algorithm, C(A) < C(B) is always true.
If A & B occur in two different processes, and they happen independently i.e. there is no causal relationship between them, C(A) and C(B) cannot be correlated and are hence considered concurrent.
Total Order Using Lamport Clocks
We can derive total ordering based on Lamport times, assuming certain priorities amongst our processes/nodes.
{ a — ( b } => { C(a) < C(b) | ( C(a) = C(b) & Pi(a) < Pj(b) )
where — ( = Total Ordering
The above states that we can define total ordering if a is an event on process Pi and b is an event on process Pj. We can establish a total order if Lamport time of a and b are different i.e (if C(a) < C(b) then in total order we can say a < b. & if C(a) > C(b) then in total order we can say b < a) OR if Lamport time of a & b are the same, and we rely on some priority of the processes/nodes to determine the order.
Shortfalls in Lamport Clock
We can establish using Lamport Clocks that if two events are causally related(A happens before B), the Lamport times for those events will always follow C(A) < C(B). However, the converse isn’t true & hence we cannot use Lamport Times to derive the causal order between events.
If you look at the picture attached, Message M5 and Message M4 are not causally related, and hence we can only assume they happened in parallel, while in reality, M5 arrived before M4(based on the physical time concept).
Also, it's possible that two events on different nodes can have the same Lamport times i.e. C(A) = C(B), but they might not have happened concurrently. This is again because each node maintains its counter. We can uniquely identify the events, however, using a combination of the Node/Process name and the Lamport Time.
This brings us to the end of this article. We learned that Lamport Clocks can help in establishing the ordering of operations, eliminating the need for physical clocks and avoiding the skewness issues associated with Physical Clocks. However, we saw that there are some shortfalls in Lamport Clocks, especially concerning ordering concurrent operations.
What’s the solution? We’ll cover that in our next article.