Beating Tail Latency: How Golang Supercharges SwissTables with Extendible Hashing
Extendible hashing is a dynamic hashing technique that allows the hash table to grow and shrink gracefully as data is added or removed, without requiring a full reconstruction of the entire table.
In our last article, we dived into SwissTables and why they’re highly performant compared to traditional HashTables. In this article, we’ll dive a bit more into how Go optimises SwissTables even more!
Problem with SwissTables:
When a hash table reaches its maximum load factor(%age of the table that’s filled before a resize operation is needed), it needs to grow the backing array. Generally, once the load factor is reached, the underlying array is doubled in size.
Now you can imagine your map insert operations running extremely fast for most operations, however, some operations that involve the resize take more time(especially for large maps like 1GB or more). This has an impact on the tail latencies, which might not be acceptable in low latency environments.
Extendible Hashing:
Extendible hashing is a dynamic hashing technique that allows the hash table to grow and shrink gracefully as data is added or removed, without requiring a full reconstruction of the entire table. It achieves this using a clever two-level structure:
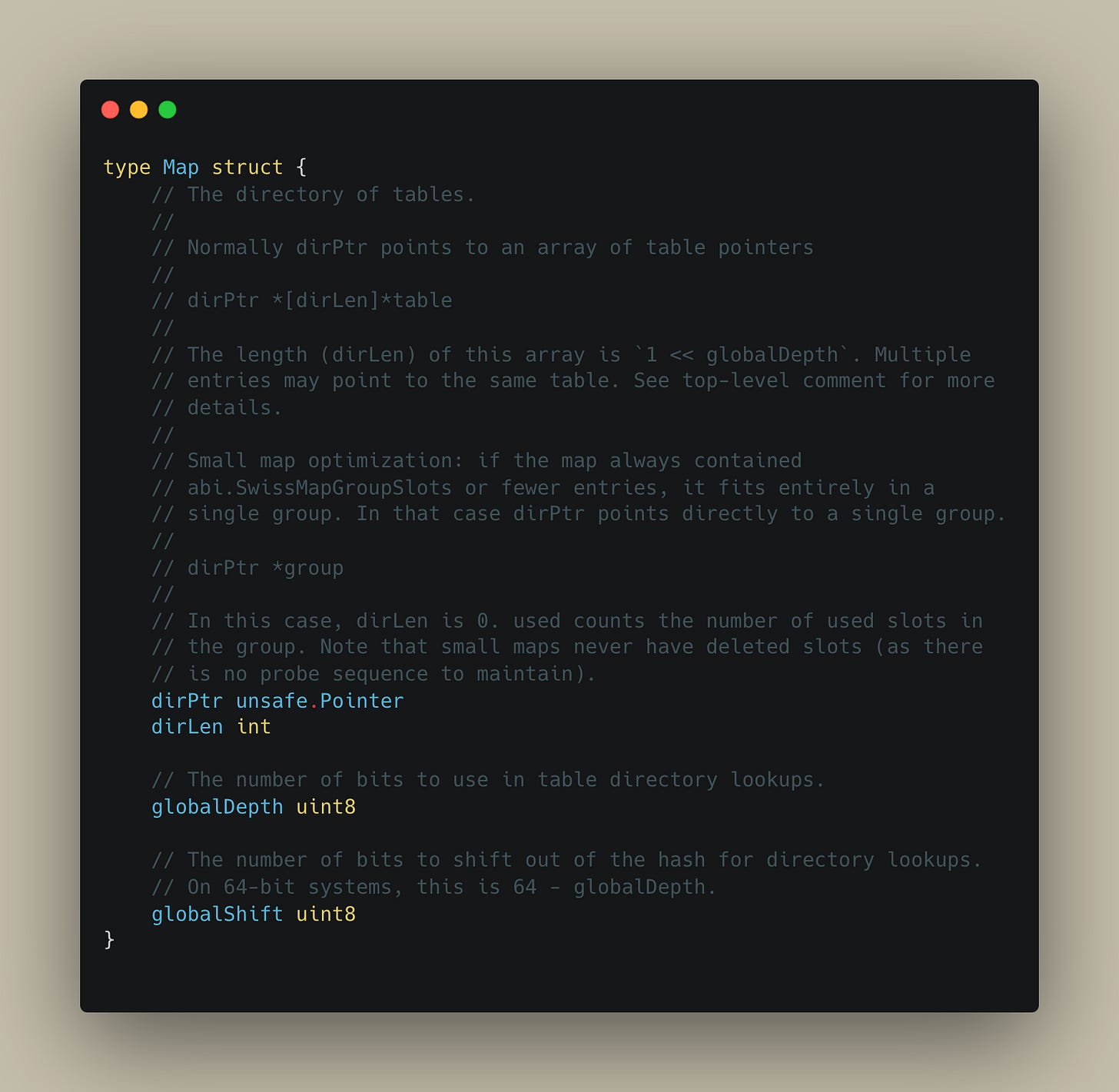
Directory: This is like an index or a table of contents. It doesn't store the data itself, but rather pointers to the actual data "array". The size of this directory can double or halve.
Data Pages: These are the actual “SwissTables” that store the key-value pairs.
So now, instead of a single SwissTable implementing the entire map, Golang splits each map into multiple SwissTables internally.
Each SwissTable has a cap of 1024 entries by default. Thus the upper bound for a single insertion is the latency of growing a 1024-entry table into two 1024-entry tables, copying 1024 entries.
Re-Sizing Magic:
The magic of extendible hashing is in the way, the hash table is resized, both at the individual hash table as well as the Directory.
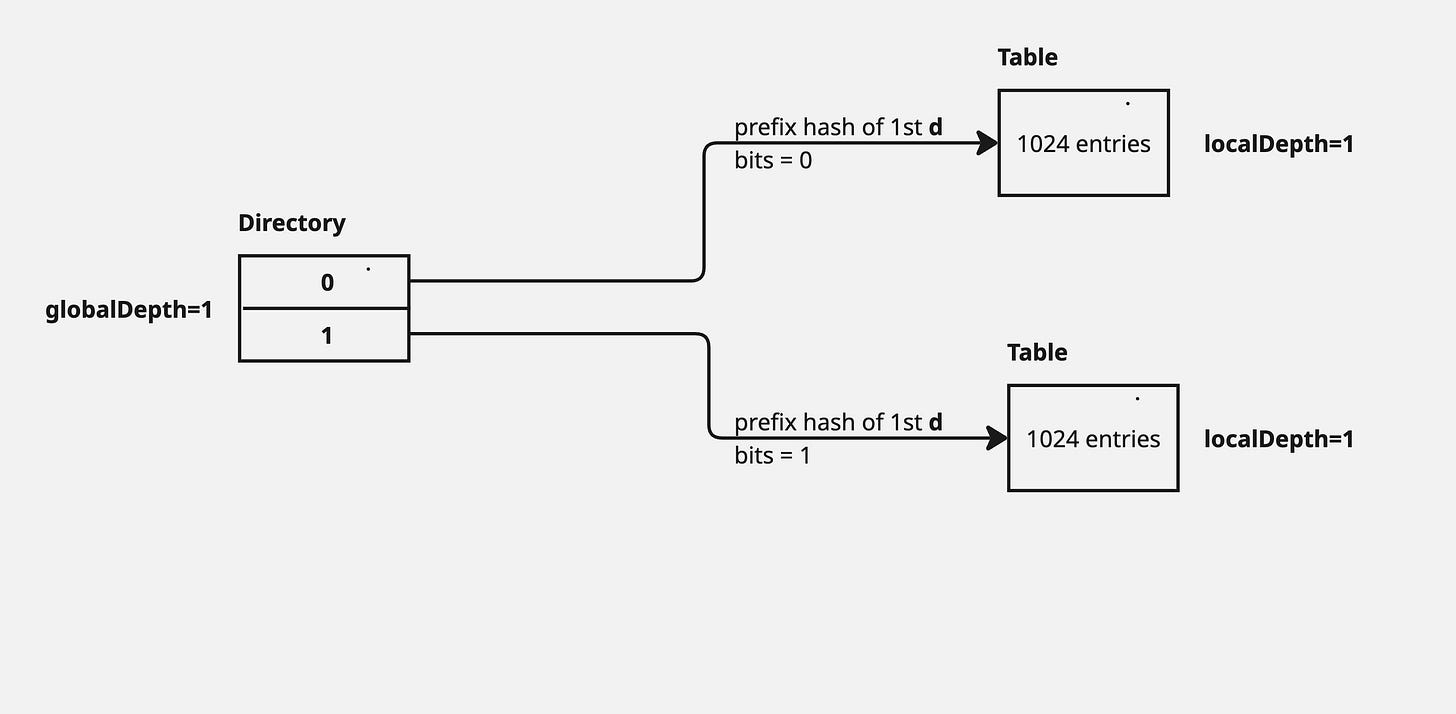
Instead of using the entire hash value of the key at once, it looks at a certain number of bits from the beginning of the hash – let's call this the global depth (d). The size of the directory is 1 « globalDepth i.e. 2^d entries.
Each SwissTable also has a local depth (d′), which tracks the depth at which they were created. The local depth will be 1 to begin with, and will increase by 1 for every split operation. All keys within a particular bucket will share the same first d′ bits in their hash value.
Once the individual data pages/SwissTables reach their defined threshold, a split operation occurs. A split creates two child tables, left and right, increasing the local depth of the newly created child tables by 1.
When a bucket overflows:
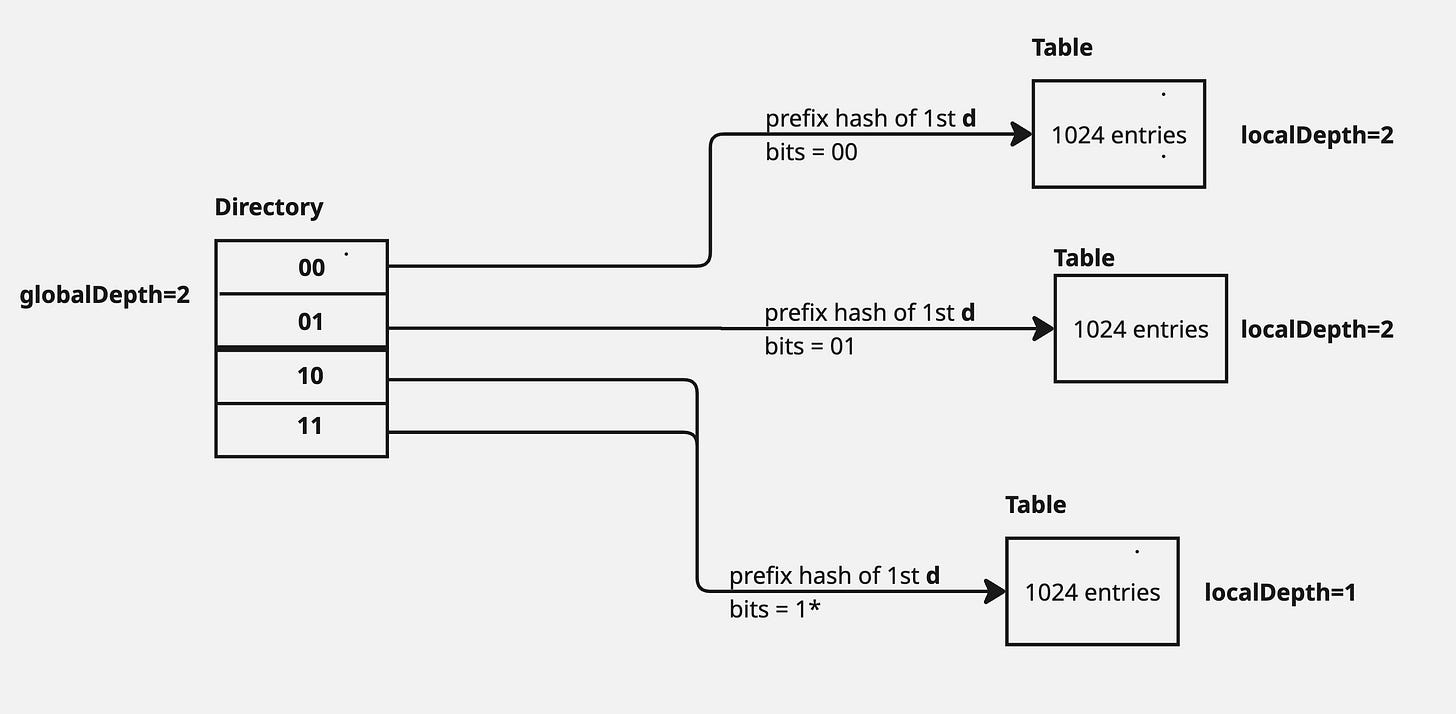
If the bucket's local depth (d′) is equal to the global depth (d), it means the directory itself isn't granular enough. So, the directory doubles in size (incrementing the global depth, d←d+1), and then the overflowing bucket is split, and its local depth is also incremented.
In the above diagram, a new insert of key, whose prefix hash started with 0, caused the Table to overflow. This created 2 tables, each with capacity of 1024 and with a local depth of currentLocalDepth + 1 i.e. 1+1=2. The directory table also doubled in size and it’s pointers needed to be updated to point to the newly created tables.
Note that multiple entries in the directory map to the same table. This is a common scenario in case the local depth(d’) is less than the global depth(d).
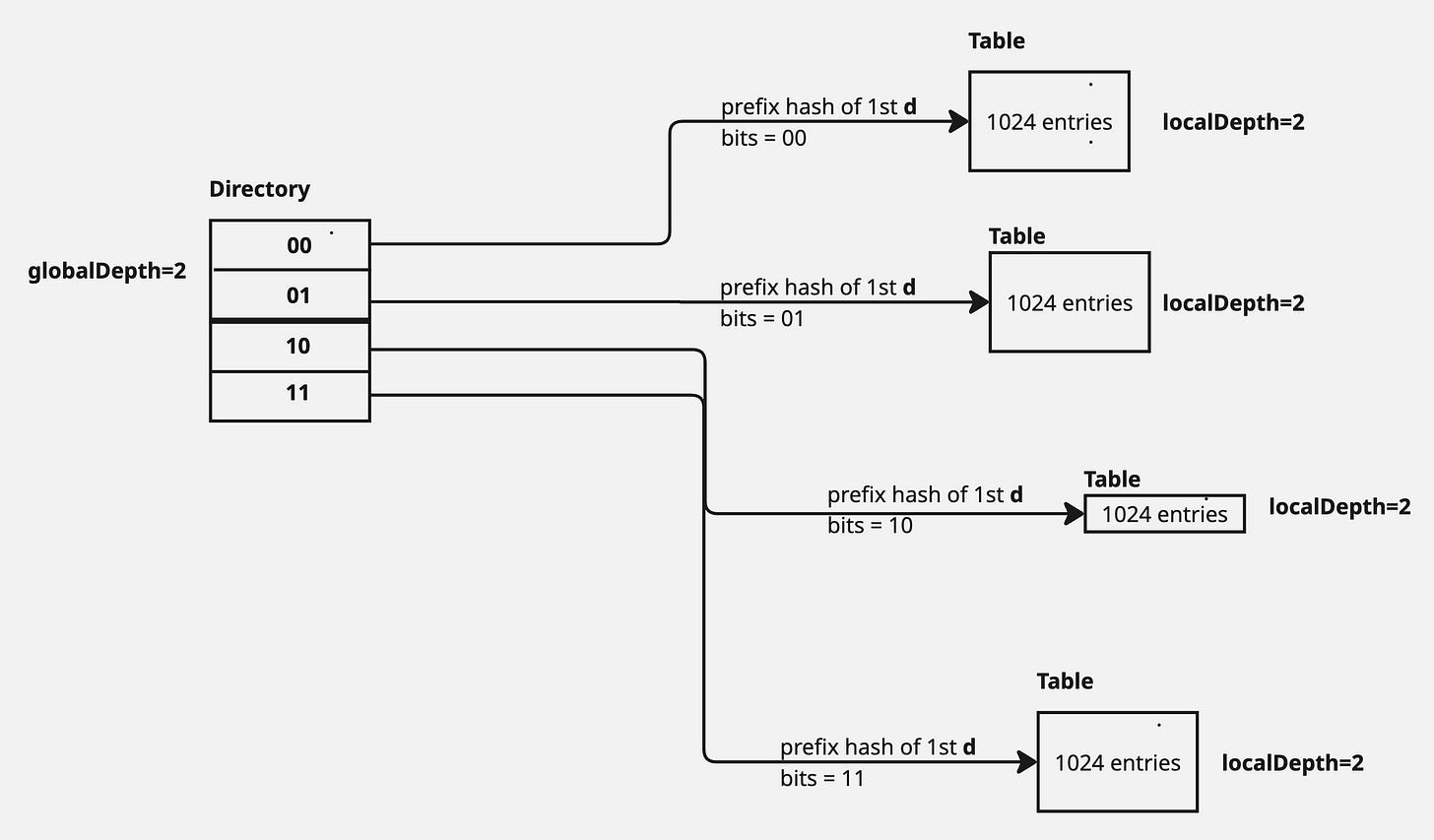
If the bucket's local depth (d′) is less than the global depth (d), the bucket is split, its local depth is incremented (d′←d′+1), and the directory pointers are updated. No need to grow the directory itself yet.
In the above diagram, a new insert of key, whose prefix hash started with 1, caused the Table to overflow. This created 2 tables, each with capacity of 1024 and with a local depth of currentLocalDepth + 1 i.e. 1+1=2. However, only the directory pointers were updated in this scenario without any change to the directory size.
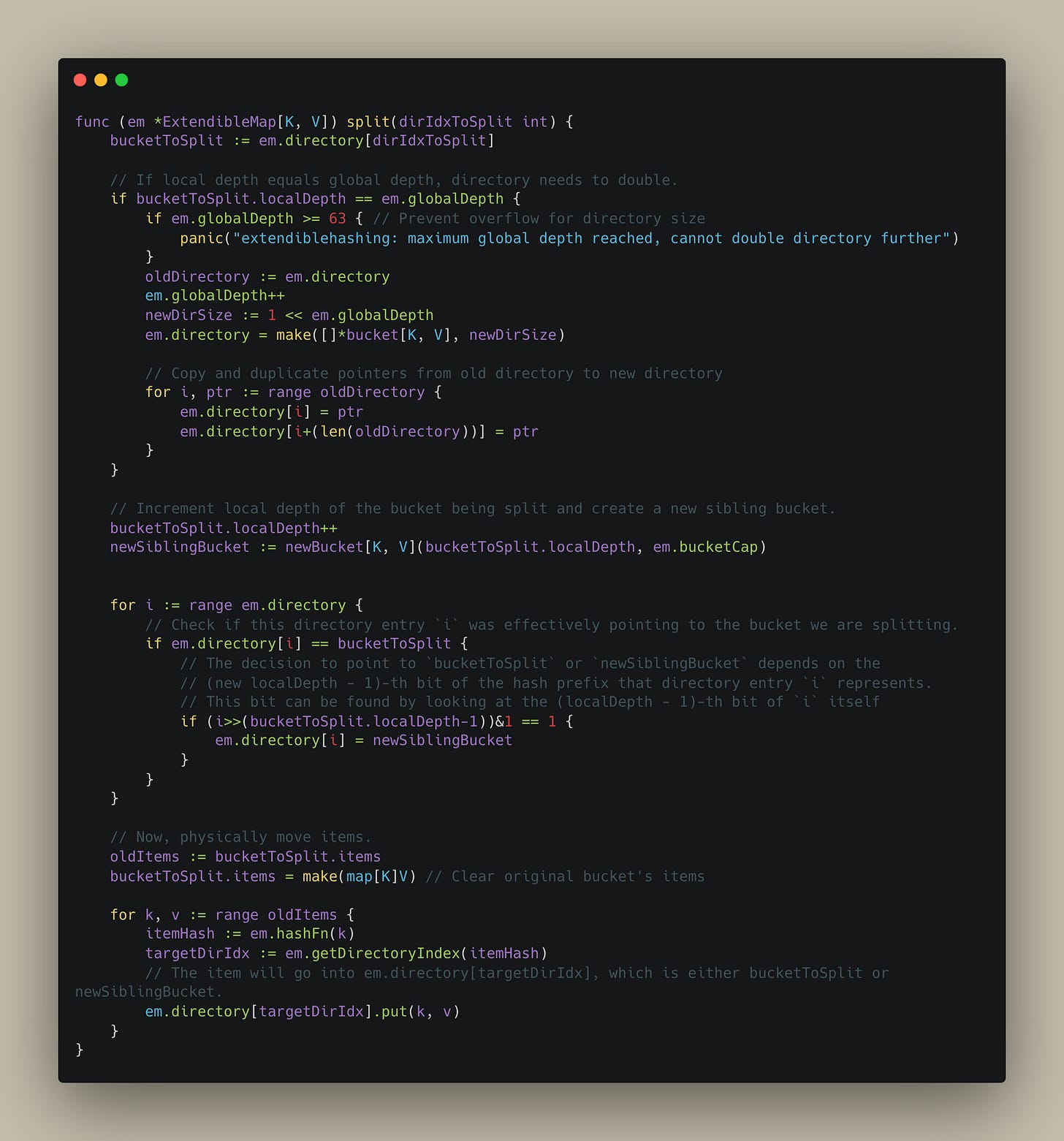
Below is a sample implementation of how the split process will work in Extendible hashmap -
Also, as promised, here’s a link to Github to my toy implementation of replicating extendible hashing.
The solution above isn’t perfect, and exposed me to the challenges while doing the split. Mostly the challenges are around how well the data gets distributed, which is influenced by the quality of your hash function. I’ll continue playing around with it and share my learnings.
This concludes this article on the Swiss Tables optimisations in Golang! Hopefully, this article gives you a good idea about extendible hashing and how it solves the problem of increasing tail latencies during large HashTable splits!
It also provides a good insight into designing good systems with predictable performance. This is a pattern I’ve followed as well in some of my systems as well.
References:
https://go.dev/blog/swisstable
https://www.dolthub.com/blog/2023-03-28-swiss-map/
https://huizhou92.com/p/swiss-map-in-go-124-compatibility-extendible-hashing-and-legacy-issues/